An Hommage to Feynman’s Technique

Fragile Knowledge

I don’t know what’s the matter with people: they don’t learn by understanding; they learn by some other way - by rote, or something. Their knowledge is so fragile!

– Richard P. Feynman

One key to successfully mastering a new subject, I believe, is to connect it to something that you are already deeply familiar with. This idea is as old as human learning and a common quality of great lecturers is that they fully embrace its logical conclusion: When introducing an audience to any novel concept, start out by conveying the main ideas in analogies and metaphors rather than drowning them in complexities and details.

And while people tend to agree that this is a good quality in a teacher, they often deprive themselves of this luxury when learning on their own. Admittedly, explaining a new idea well to yourself requires a substantial amount of additional effort. However, I am convinced that this overhead is not only economical but of fundamental importance if you ever plan to master a new set of skills (as opposed to gaining the mostly worthless knowledge of sparsely connected facts).

Case Study: Understanding Neural Networks

So, if you are still with me, I’d like to demonstrate how this might look like when first learning about neural networks. Basically I’ll try to reconstruct the inner monologue that went through my head when I just first learned about them.

“Neural networks are basically directed graphs with metadata. Nodes represent neurons, edges represent the data-flow between those neurons and the metadata comes in two flavours:

1. The weight attached to every edge determines how much of an influence its source neuron has in the overall network and

2. An activation function, attached to each neuron, that determines the ‘shape’ of this neuron’s discharge pattern. ¹

So far, so good. But what does that mean? How can a neural network process information?”

Stepping out of character for a second: It’s here that you can make life very difficult for yourself. Both leaving this question unanswered and jumping into some complex example (e.g. ResNet) are, in my opinion, terrible mistakes. You want to build a simple example, ideally relying only on yourself, for two reasons:

1. First and most importantly: This is a litmus test. If you are not able to build a basic example of the concept you’ve just learned about, you haven’t understood the basics yet and need to revisit them. By forcing yourself to sit down and actually spelling out a very simple example in detail, you’re making sure that your previous gained confidence is justified and that you’re not just fooling yourself.

   The first principle is that you must not fool yourself – and you are the easiest person to fool.

   – Richard P. Feynman

2. If you want to master any subject, it is my firm opinion that you must carry around a large set of examples in your head. These examples will not only guide your intuition but they will also serve as a more and more elaborate testing ground for new ideas. In the future, if someone tells you about some new fancy concept (that someone might be you), you can refer to an appropriate example in your head and see how it would influence that. If the results don’t make sense, something’s wrong! Either you’ve misunderstood what the other party is telling you or there is a mistake. Assuming you want this conversation to remain meaningful, you need to fix that! This is how I, and how I believe most of my colleagues, are able to build an appropriate intuition about complex concepts that often run counter to any experience you might have had in your daily life.

   Building a simple example from scratch is your first step toward assembling your internal database.

Okay, let’s return to the inner monologue:

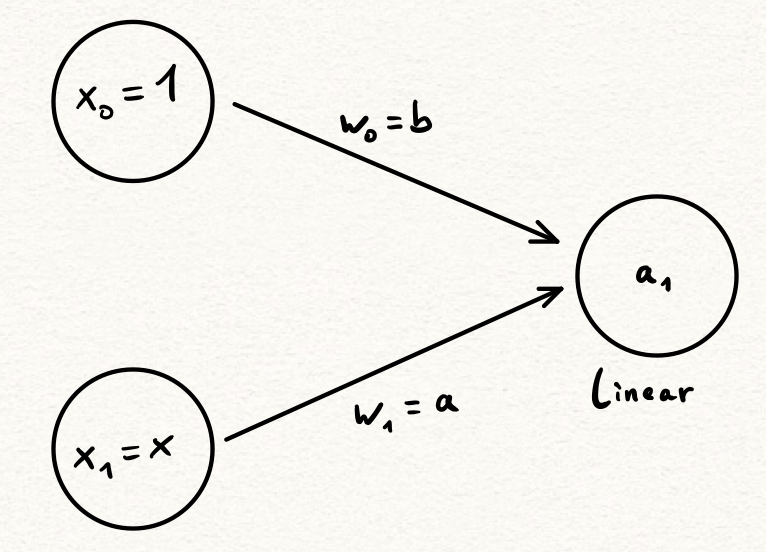
“Is there anything I already know about that could easily be realized as a neural network? Actually, yes: Linear functions are of the form \(f(x) = a \cdot x + b\) and they are represented by the following neural network: ²

Great, but how about logical connections? If artificial neural networks are supposed to model actual neural networks, they certainly must be able to capture logic gates, right? Right!

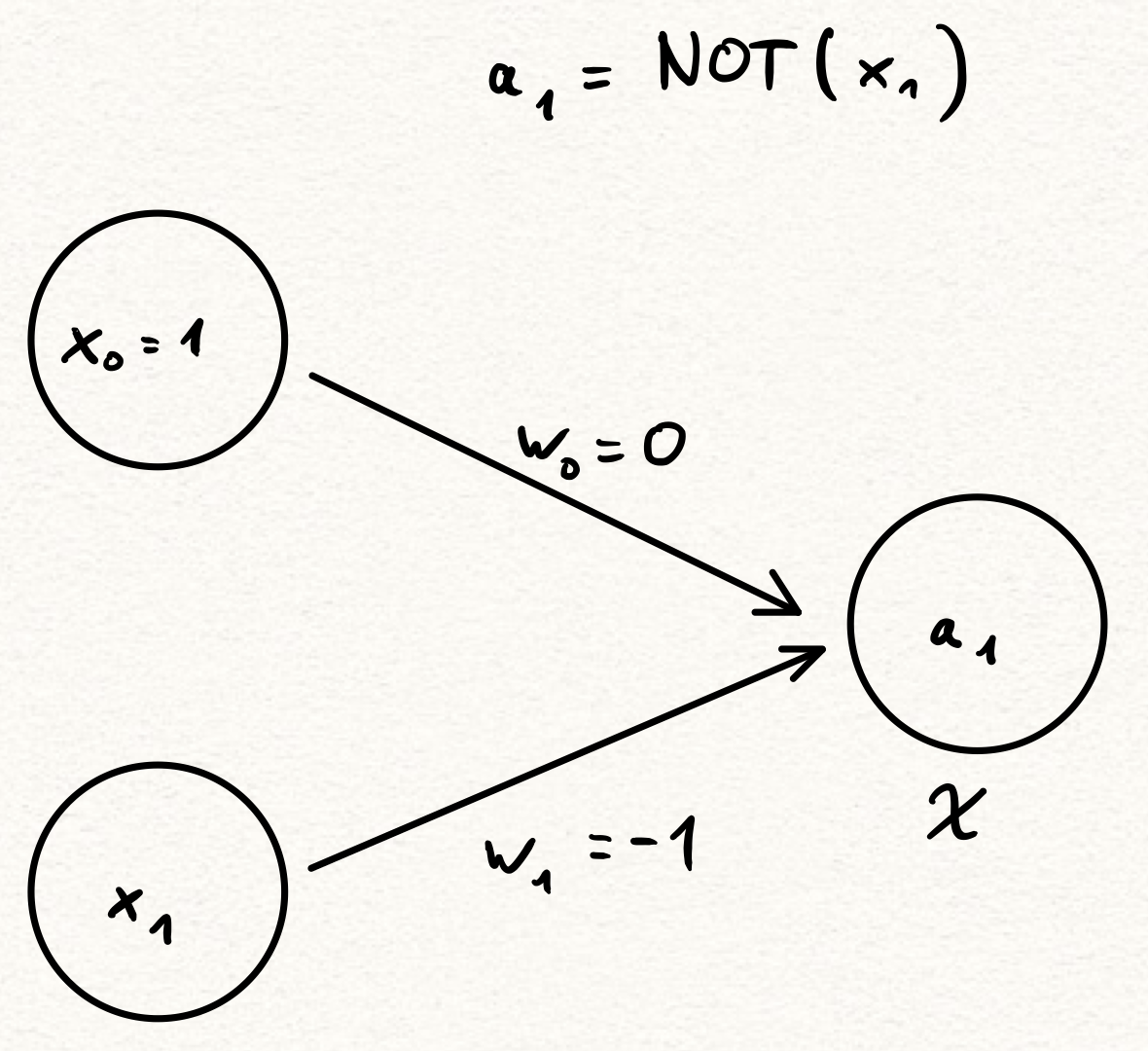
Here \(\chi = \chi_{[0, \infty)}\) is the activation function of \(a_1\) and all you need to know is that \(\chi(z) = 0\) for all \(z < 0\) and \(\chi(z) = 1\) for all \(z \ge 0\). So, if we set \(x_1 = 0\), we get that \(a_1 = \chi(w_0 \cdot x_0 + w_1 \cdot x_1) = \chi(0 \cdot 1 + (-1) \cdot 0) = \chi(0) = 0\). On the other hand, if we let \(x_1 = 1\), we get that \(a_1 = \chi(0 \cdot 1 + (-1) \cdot 1) = \chi(-1) = 0\). So this neural network does indeed represent \(\mathrm{NOT}(x_1)\)!”

At this point, you might want to cook up a few more examples and in an earlier tweet I demonstrated how to represent other basic logic gates (AND, OR, NOR, XOR, XNOR) as neural networks as well. I’d encourage you to try it yourself first and then hop over to Twitter and compare your results with mine. ³

Once you’ve done that, you may notice what I’ve noticed: Not only can neural networks represent logic gates. Neural networks are nothing more than logic gates, with a few minor adjustments:

1. Inputs are allowed to take on any real number as value, not just \(0\) and \(1\),

2. We add a restriction that a node’s value is computed by a weighted, linear combination of the values to its left followed by an activation function and

3. We add an activation functions to our nodes. ⁴”

It may not seem that way, but this little detour is incredibly beneficial to your overall learning strategy. Ideas and memories die in a vacuum. If you want them to become lasting and meaningful, you need to them connect to as many previously established ideas as possible. Don’t believe me? Then tell me: What did you have for dinner last Wednesday? Unless you are able to connect last Wednesday’s dinner to something more meaningful (maybe you happened to be on a first date), most of us will struggle mightily with this very simple question. And if I ask you about your lunch a year ago, there’s basically no chance you’ll be able to remember. On the other hand, if I ask you what you did last Christmas (or even better: On your wedding day if you happen to be married), the task becomes much easier. You either connect ideas and memories or you will lose them – quickly. Not only that: Sparsely connected ideas (what Feynman calls ‘fragile knowledge’) are basically worthless as they’re not readily available to be used in similar, but slightly different, settings.

What you should take away from this

If you make a habit of always explaining new ideas to yourself until you’ve completely broken them down to related concepts, that you’ve already mastered, you’ll never have to learn or memorize anything truly novel again. And, over time, you’ll gain firm, deeply connected, foundational knowledge about seemingly unrelated concepts that will not only help you to learn other concepts faster and more efficient but, ultimately, also allow you to solve problems in surprising, efficient and truly ingenious ways. Being able to do that is, in a nutshell, the mark of a true expert.

1. I think it’s helpful to point out that this is one of the ways that artificial neural networks differ from biological ones. Biological neurons either fire or they don’t – so, in a way, the only activation function they’re allowed to have is the characteristic function \(\chi_{(-\infty, a]}\) for some number \(a\). ↩

2. This follows Andrew Ng’s handy convention that any neuron/weight with a \(0\) as subscript represents a bias component – independent of the input. ↩

3. In case you don’t want to use Twitter, you can find my solution here ↩

4. This point, in theory, is incredibly powerful. In fact, it’s too powerful. Since neural networks are intended to approximate some function \(f\) to begin with, we could always achieve this by taking \(f\) as our activation function. In practice, however, \(f\) is unknown, we only allow activation functions from a very restrictive, simple set of functions and their specific choice, in many cases, turns out to be surprisingly irrelevant. ↩