TensorFlow Without Tears

Life is pretty crazy right now. Finishing a PhD, changing from set theory to applied data science, forming connections to other data scientists, learning as much about machine learning (both theory and practice) as I possibly can, finding a new apartment and preparing to move, dealing with German bureaucracy… This doesn’t leave a lot of spare time. Truth be told, it doesn’t leave any.

I’m not complaining – the last couple of months have been immensely enjoyable (well, except for the bureaucracy part). But being pressed for time also made me decide to postpone my planned blog series on the importance of probability distributions in machine learning as I’m currently lacking the spare mental capacity to do this rather broad, open-ended topic justice.

TensorFlow 2

Instead, to finally return the ball of machine learning conversation to my readers, I’d like to share my excitement about TensorFlow 2. The beta of TF2 has been announced 4 days ago and while I didn’t take part in the alpha at all, I’ve set aside a bit of time over the weekend to play around with the newly released beta. And it’s been incredibly exciting!

See, what often sets me apart in a group of people is that I really like to get down to the nuts and bolts of anything I lay my hands on. As a young child I’ve disassembled pretty much every electronic device in our household, I’ve worked on charmingly simple cars by the time I graduated from kindergarten, I’ve spent most of my childhood in the workshop of my grandfather. This hands-on, detail-focused, borderline obsessive personality trait never left me.

And it’s precisely what made me fall in love with TF1 when I first discovered it. TF1, at least to me, isn’t really a machine learning framework at heart. Admittedly, it has a bunch of utilities built into it that are useful in machine learning applications, but what TF1 does at its core is to provide a framework for the manipulation of dataflow graphs. This philosophy makes TF1 very versatile, performant and transparent. But it also sets up a learning curve that, especially to someone without a background in mathematics or computer science, looks more like a learning wall. And like so many other learning walls (vi anyone?), it naturally turns away a lot of people. Especially those people that I’ve benefited the most from during my entire life: People who, unlike me, don’t care much about bolts and nuts but who naturally focus much more on the greater picture, who provide a sense of style, a desire for polish that benefits the entire community.

Keras has done a lot to attract a more diverse group of users to TensorFlow 1. To quote their FAQ:

Keras prioritizes developer experience

• Keras is an API designed for human beings, not machines. Keras follows best practices for reducing cognitive load: it offers consistent & simple APIs, it minimizes the number of user actions required for common use cases, and it provides clear and actionable feedback upon user error.
• This makes Keras easy to learn and easy to use. As a Keras user, you are more productive, allowing you to try more ideas than your competition, faster – which in turn helps you win machine learning competitions.
• This ease of use does not come at the cost of reduced flexibility: because Keras integrates with lower-level deep learning languages (in particular TensorFlow), it enables you to implement anything you could have built in the base language. In particular, as tf.keras, the Keras API integrates seamlessly with your TensorFlow workflows.

This amazing body of work has enabled TF2 to pull off what so rarely seems attainable: By embracing Keras’ philosophy, TF2 became a piece of software that is both user-friendly and still provides all the functionality, all the performance and all the transparency any user could ask for. This almost never happens but when it does, it makes me really, really happy.

Hello, I’m TensorFlow.

In an effort to invite as many people as possible to share my excitement about TF2 and join the discussion, I’d like to end this post with a very simple regression task completed in TensorFlow 2. We aim to approximate the function \(\sin \colon [0, 2 \pi] \to [-1, 1], x \mapsto \sin (x)\) with a neural network. You can find the interactive Jupyter notebook over at Google Colaboratory or just continue reading for a slighly more verbose version.

The first part of any machine learning project is to load our dependencies.

!pip install tf-nightly-2.0-preview
import tensorflow as tf

import numpy as np
import matplotlib.pyplot as plt

Next, we load our data. In this case, to keep things as simple as possible, we will simply create the sine function on the interval \([0, 2 \pi]\) and approximate it.

x = np.arange(0, 2 * np.pi, 2*np.pi / 10000)
y = np.sin(x)

When possible, it’s always a good idea to look at a visual representation of your data. This serves as a baseline sanity check to ensure there is no immediately obvious problem.

plt.plot(x,y)

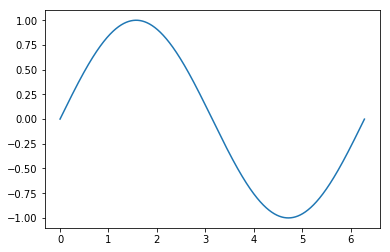
That looks okay, so let’s continue by building our neural network. The integration of Keras makes this very simple:

# Build a neural network with 2 hidden layers, each of size 128
model = tf.keras.models.Sequential([
    tf.keras.layers.Dense(128, activation='relu', input_shape=[1]),
    tf.keras.layers.Dense(128, activation='relu'),
    tf.keras.layers.Dense(1, activation='linear')
])

Compiling the model is similarly trivial.

model.compile(optimizer='adam',
              loss='mean_squared_error',
              metrics=['accuracy'])

Finally, let’s fit the neural network to our training data.

model.fit(x,y, epochs=5)

Train on 10000 samples

Epoch 1/5 10000/10000 [==============================] - 1s 72us/sample - loss: 0.1698

Epoch 2/5 10000/10000 [==============================] - 1s 61us/sample - loss: 0.0904

Epoch 3/5 10000/10000 [==============================] - 1s 58us/sample - loss: 0.0415

Epoch 4/5 10000/10000 [==============================] - 1s 53us/sample - loss: 0.0109

Epoch 5/5 10000/10000 [==============================] - 1s 52us/sample - loss: 0.0023

<tensorflow.python.keras.callbacks.History at 0x7fa30305c5f8>

That’s it! We’ve created and successfully trained a neural network to approximate the sine function on \([0, 2 \pi]\) and the training output seems encouraging. All that’s left to do is to visualize how well we’ve done:

pred = model.predict(x)
plt.plot(x,pred, label='model prediction')
plt.legend()

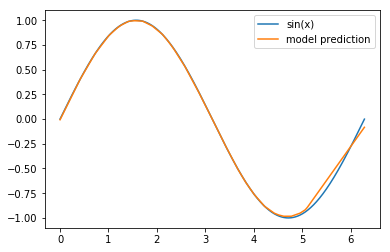
Not bad, not bad at all! The interval \([5,2 \pi]\) needs some work (and I encourage you to think about why our model performed so much worse on that section) but other than that, I’d say that our model does know how to create a sine wave.

I’ve decided to give a few hints as to why our model performs worse on the tail end of our data set: Consider the following animation of the learning process

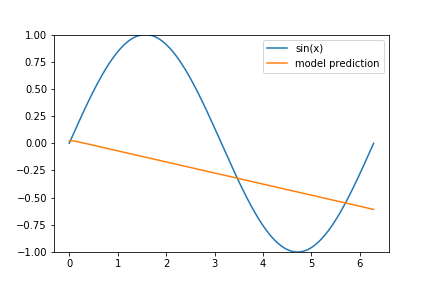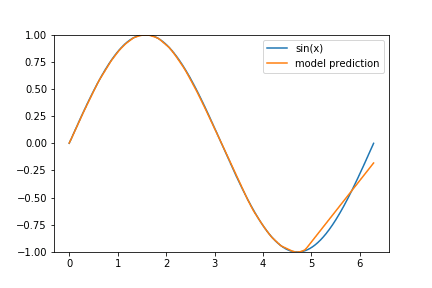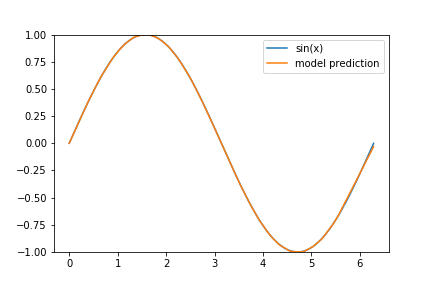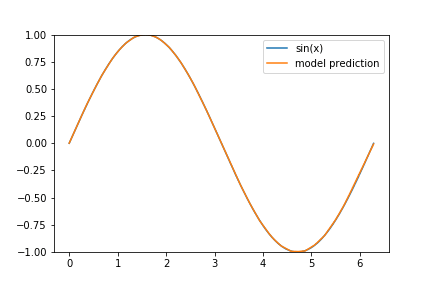
and keep in mind that we are using the ‘Adam’ optimizer.